教員詳細
-

-
加葉田 雄太郎 Yutaro KABATA
- メールkabatanagasaki-u.ac.jp- 役職・取得学位 総合生産科学域 助教
情報データ科学部 助教
博士(理学)- 専門分野 特異点論、曲線・曲面論、応用特異点論- 外部リンク researchmap
就職実績 ― 民間機関、他大学等(略歴)
| H24.3 | 国際基督教大学 教養学部 卒業 |
| H26.3 | 北海道大学大学院 理学院 数学専攻 修了(修士) |
| H29.3 | 北海道大学大学院 理学院 数学専攻 修了(博士) |
| H29.4 | 神戸大学大学院理学研究科数学専攻 日本学術振興会特別研究員PD |
| H30.4 | 北海道大学電子科学研究所附属社会創造数学研究センター 学術研究員 |
| H30.5 | 九州大学マス・フォア・インダストリ研究所 兼 数理・データサイエンス教育研究センター 特プロ助教 |
研究活動
特異点論、曲線・曲面論
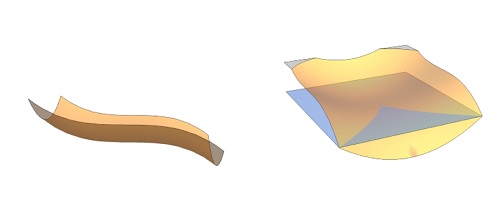
特異点論に関する数学的基礎研究が主要研究の一つである。大雑把に言って、特異点とは対象に現れる他とは異なる特別な点のことであり、数学に限らず諸科学の様々な現場で現れる。私は特に、可微分写像に現れる特異点の幾何的な性質を研究することや、特異点論の道具を用いて曲面や曲線の局所的な性質を研究することに取り組んでいる。

応用数学
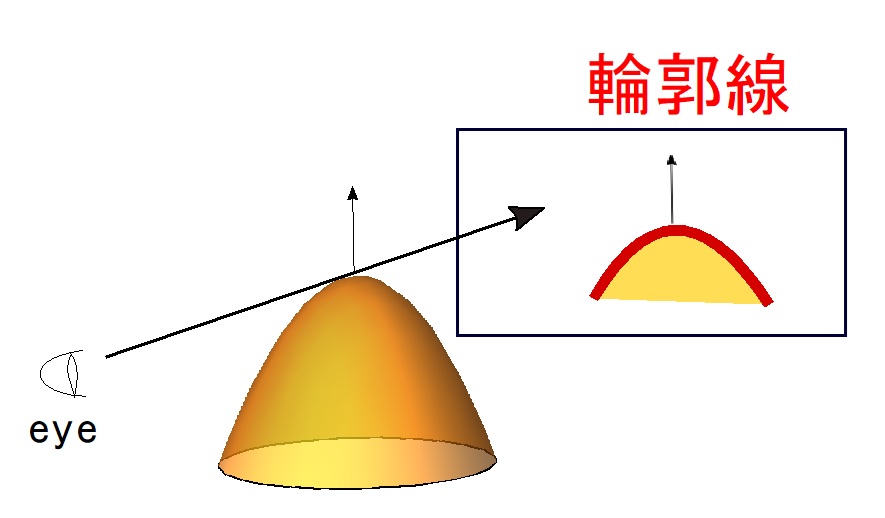
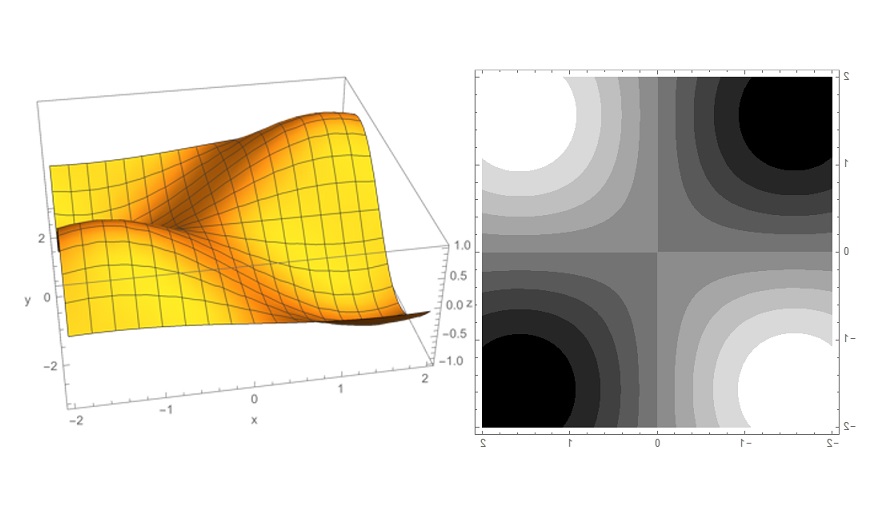
特異点論を応用した曲面や曲線の研究は視覚の数理に関する研究とも非常に相性が良い。例えば、滑らかな物体を見た時の輪郭は、滑らかな曲面の平面への射影の写像の特異点集合と考えることができ、写像の特異点論を応用して研究することができる。また、種々のデータの背後には広い意味での曲面的な構造が存在して、データの特徴は曲面としての不変量によって捉えられるという事例は多い。特にデータの特徴点の発見や解析は特異点論と非常に相性が良いと考えている。このような数学の応用テーマでの実践的な研究成果を目指して、様々な異分野共同研究にも取り組んでいる。
教育活動
担当授業
情報データ科学部:微分積分学Ⅱ
